Mathematica stellt jedes Objekt als symbolischen Ausdruck dar.
Alle symbolischen Ausdrücke ergeben sich als Kombinationen des Basisausdruckes der Form: head[![]() ,
,![]() ,…]
,…]
Eine Liste von Elementen:
![]()
![]()
Ein algebraischer Ausdruck:
![]()
![]()
Grafik:
![[Graphics:HTMLFiles/index_7.gif]](HTMLFiles/index_7.gif)
![Graphics[{Circle[{1, 0}, 2], <br /> &nb ... bsp; Circle[{-1, 0}, 2]}]](HTMLFiles/index_8.gif)
Ein button:
![]()
![]()
Eine Zelle in einem "notebook":
A cell containing text
![Cell["A cell containing text", "Text"]](HTMLFiles/index_11.gif)
Alle Operationen in Mathematica sind Transformationen symbolischer Ausdrücke auf der Basis einer leistungsfähigen Mustererkennung.
Mit /. führt Mathematica eine einfache Transformation b→1+x durch.
![]()
![]()
Bezeichnen x_ und y_ beliebige Ausdrücke, so ergibt der Ausdruck x_+y_ die Summe der Terme.
![]()
![]()
![]()
![]()
Mathematica verwendet Ausdrücke (patterns) zur Definition von Funktionen in der Kombination von Funktionsvorschriften und Spezialfällen.
Eine Funktionsdefinition für beliebige x (zunächst als reell vorausgesetzt).
![]()
Ein Spezialfall überschreibt die allgemeine Vorschrift.
![]()
Ein Beispiel der Anwendung von f:
![]()
![]()
Dadurch wird die Definition von f gelöscht :
![]()
In den Funktionsargumenten können allgemeine Strukturen (Zahlen, Kreise, Matritzen,...) vorkommen.
Ein Funktionswert von g ergibt sich aus Listenargumenten:
![]()
![]()
![]()
![]()
Ein Kreis kann ein Funktionsargument sein:
![]()
![]()
![]()
Trigonometrische Funktionen und Exponentialfunktionen
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Additionstheoreme für Winkelfunktionen
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![(Cos[y] Sin[x])/(Cos[x] Cos[y] - Sin[x] Sin[y]) + (Cos[x] Sin[y])/(Cos[x] Cos[y] - Sin[x] Sin[y])](HTMLFiles/index_45.gif)
![TrigFactor[Cos[x] Cos[y] - Sin[x] Sin[y]]](HTMLFiles/index_46.gif)
![]()
Drehmetrizen (analytische und algebraische Strukturen mit Mathematica)
![]()
![]()
![]()
![]()
![{{Cos[x] Cos[y] - Sin[x] Sin[y], Cos[y] Sin[x] + Cos[x] Sin[y]}, {-Cos[y] Sin[x] - Cos[x] Sin[y], Cos[x] Cos[y] - Sin[x] Sin[y]}}](HTMLFiles/index_52.gif)
![]()
![]()
![]()
![]()
![]()
![]()
Matrizen (Mathematica und algebraische Strukturen)
![]()
![]()
![]()
![]()
Produkt mit Scalaren:
![]()
![]()
nur in Mathematica:
![]()
![]()
![]()
![]()
![]()
Produkte und Potenzen
![]()
![]()
![]()
![]()
![]()
![]()
![]()
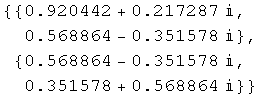
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
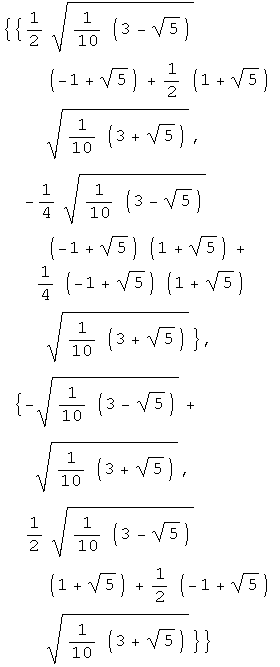
Beispiel eines diskreten Modells (Fibonaccizahlen)
Definition 1 in Mathematica:
![f[n_] := f[n - 1] + f[n - 2] ; f[0] = 1 ; f[1] = 1 ;](HTMLFiles/index_88.gif)
![]()

![]()
![]()
Definition 2 in Mathematica ("Funktion mit Gedächtnis"):
![g[n_] := g[n] = g[n - 1] + g[n - 2] ; g[0] = 1 ; g[1] = 1 ;](HTMLFiles/index_93.gif)
![]()

![]()
![]()
Zusammenhang mit Matrizenrechnung:
![MatrixPower[{{1, 1}, {1, 0}}, 29]//MatrixForm](HTMLFiles/index_98.gif)
![]()
Explizite Definition:
![h[n_] := 1/Sqrt[5] (((1 + Sqrt[5])/2)^(n + 1) - ((1 - Sqrt[5])/2)^(n + 1))](HTMLFiles/index_100.gif)
![]()
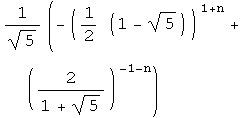
![]()

Rekurrence-Gleichungen und erzeugende Funktionen
![]()
![RSolve[{a[n] a[n - 1] + a[n - 2], a[0] a[1] 1}, a[n], n]](HTMLFiles/index_106.gif)
![{{a[n] (2^(-1 - n) (-(1 - 5^(1/2))^(1 + n) + (1 + 5^(1/2))^(1 + n)))/5^(1/2)}}](HTMLFiles/index_107.gif)
![GeneratingFunction[{a[n] a[n - 1] + a[n - 2], a[0] a[1] 1}, a[n], n, x]](HTMLFiles/index_108.gif)
![]()
![]()
![1 + x + 2 x^2 + 3 x^3 + 5 x^4 + 8 x^5 + 13 x^6 + 21 x^7 + 34 x^8 + 55 x^9 + 89 x^10 + 144 x^ ... 4 + 121393 x^25 + 196418 x^26 + 317811 x^27 + 514229 x^28 + 832040 x^29 + 1346269 x^30 + O[x]^31](HTMLFiles/index_111.gif)
![]()

![g[n_] := g[n] = g[n - 1] + g[n - 2] ; g[0] = 1 ; g[1] = 1 ;](HTMLFiles/index_114.gif)
![]()

Tensoren
![]()
![]()
![]()
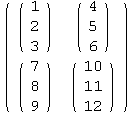
Beispiel: Berechnungen mit 1200×900×3-Tensor
![(* g = Import["c:\\vl2004\\IMGA1468.jpg"] ; Bildübertragungen sind über In ... 400, 300}] ; <br />g[[1, 1]] = gg[[1, 1]] - 100 ; <br />Show[g, ImageSize {400, 300}] *)](HTMLFiles/index_121.gif)
| Created by Mathematica (October 23, 2005) |